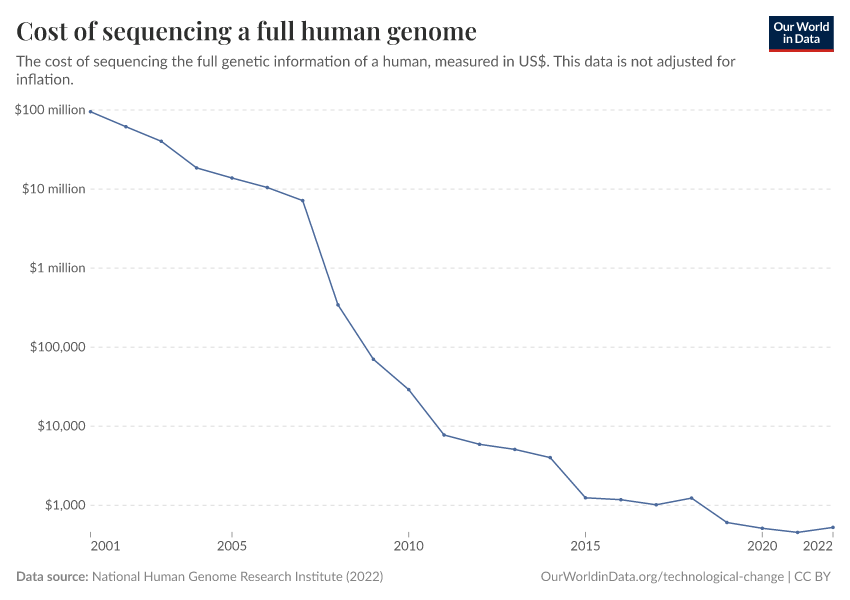
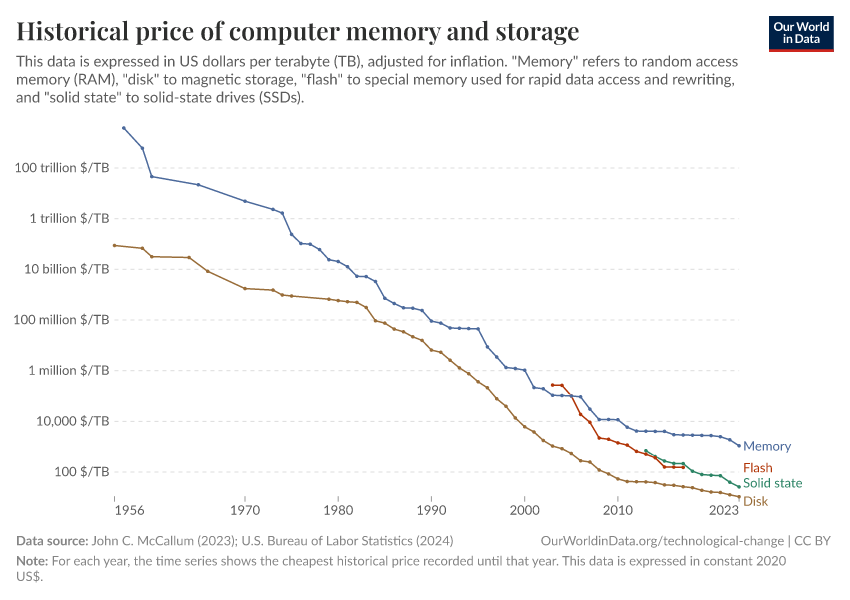
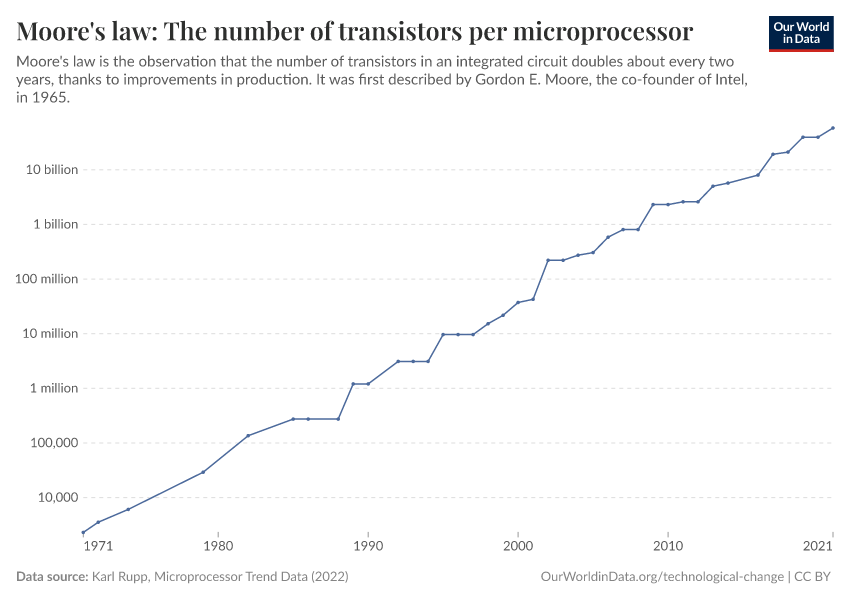
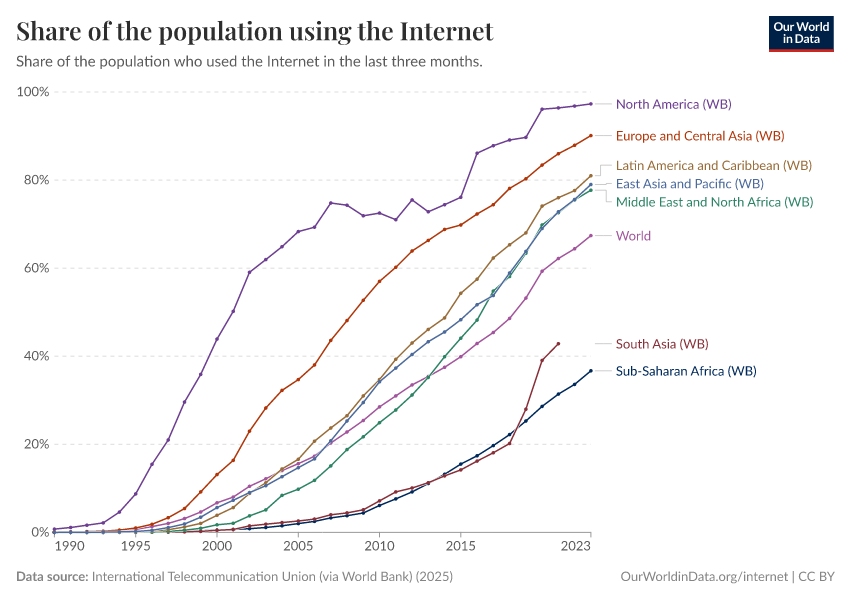
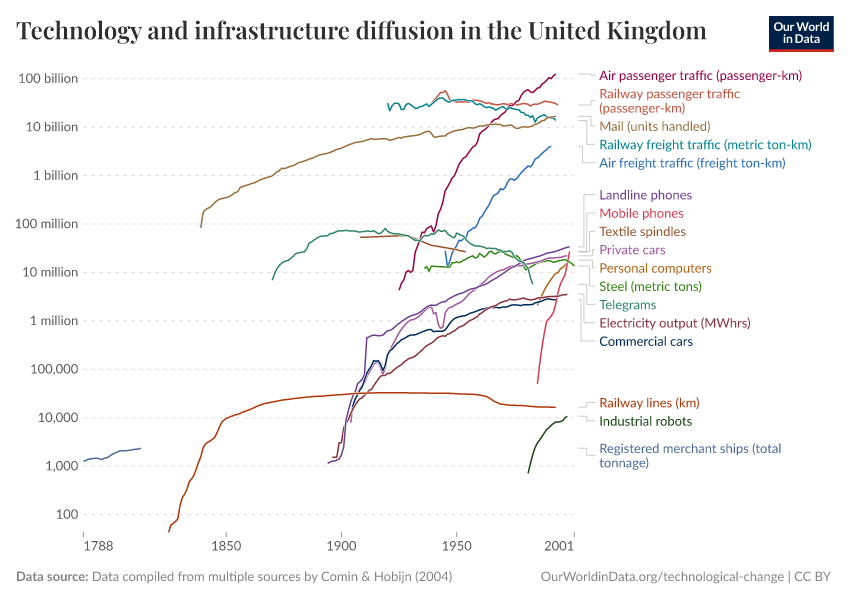
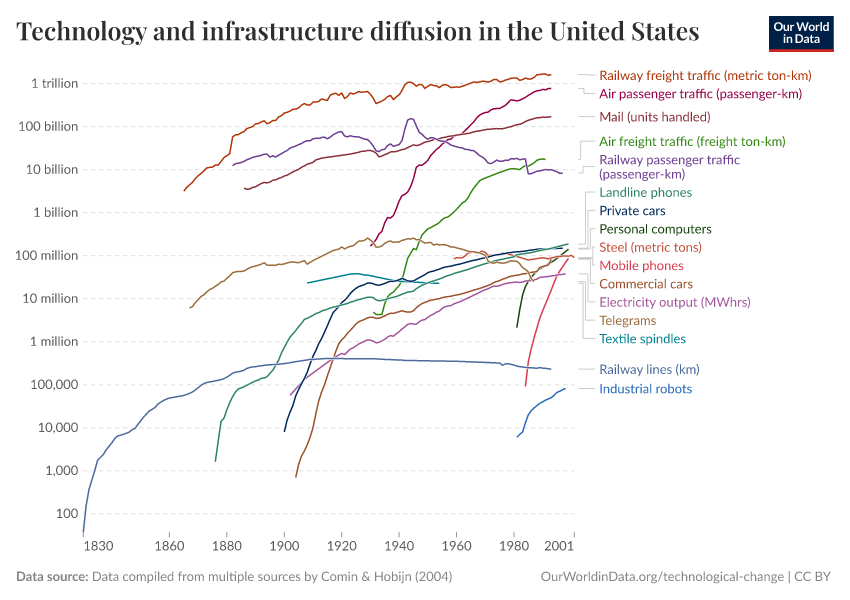
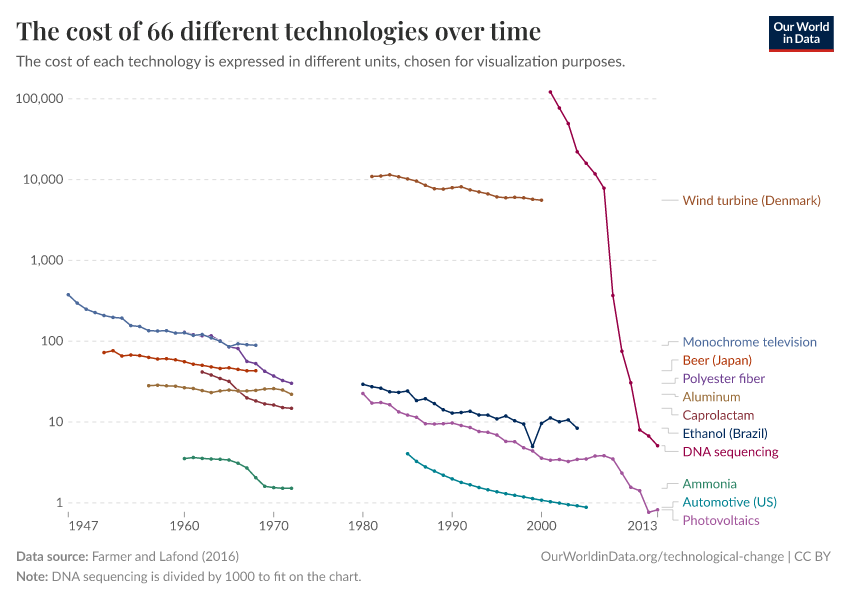
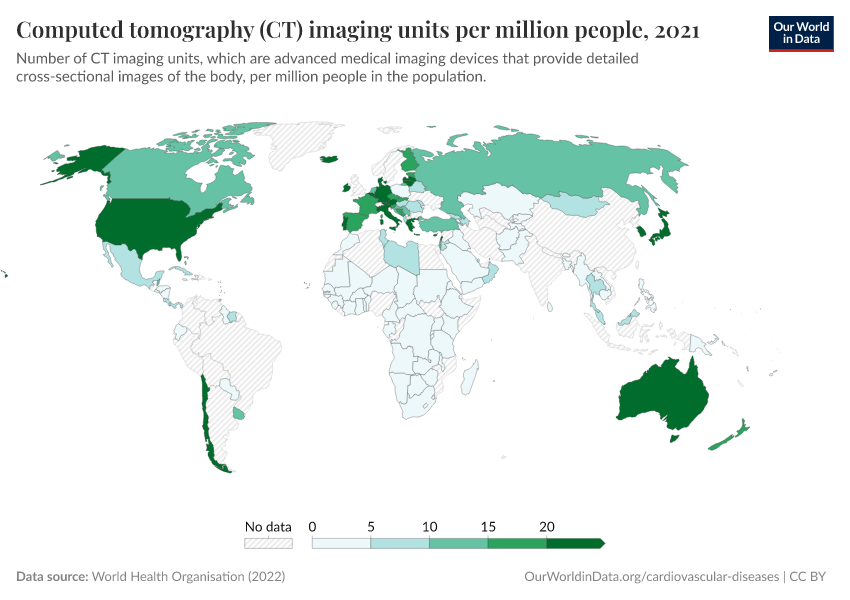
Technological Change
Technological change underpins many of the developments we've seen in health, agriculture, energy, and global development.
Almost every development we cover on Our World in Data is underpinned by technological change.
Medical innovations contributed to the decline in child mortality and the improvement in life expectancy. Thanks to the advances in agricultural technologies, higher crop yields and less undernourishment became possible. The long-term decline of global poverty was primarily driven by increased productivity from technological change. Access to energy, electricity, sanitation, and clean water has transformed the lives of billions. Transport, telephones, and the Internet have allowed us to collaborate on problems at a global level.
Emerging technologies are often expensive and, therefore, initially limited to society's richest. A key part of technological progress is making these life-changing and often life-saving innovations affordable for everyone.
Technology has improved our lives in many ways, but these developments are not always positive. Many of humanity’s largest threats — such as nuclear weapons and potentially artificial intelligence — result from technological advances. To mitigate these risks, good governance can be as important as the technology itself.
On this page, you can find our data, visualizations, and writing on the most fundamental technological changes that have shaped our world.
Research & Writing
Key Articles on Technological Change
February 22, 2023
Technology over the long run: zoom out to see how dramatically the world can change within a lifetime
December 06, 2022
The brief history of artificial intelligence: the world has changed fast — what might be next?
December 15, 2022
Artificial intelligence is transforming our world — it is on all of us to make sure that it goes well
June 04, 2021
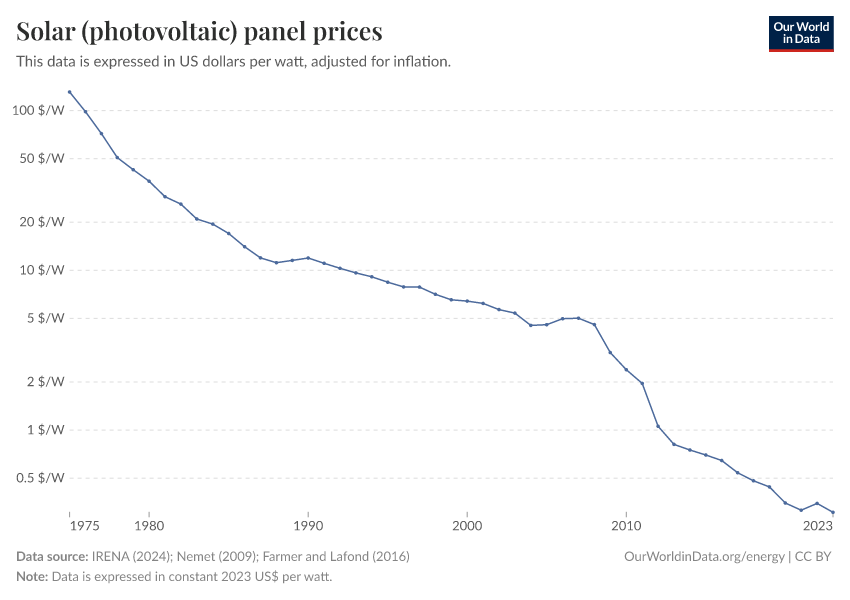
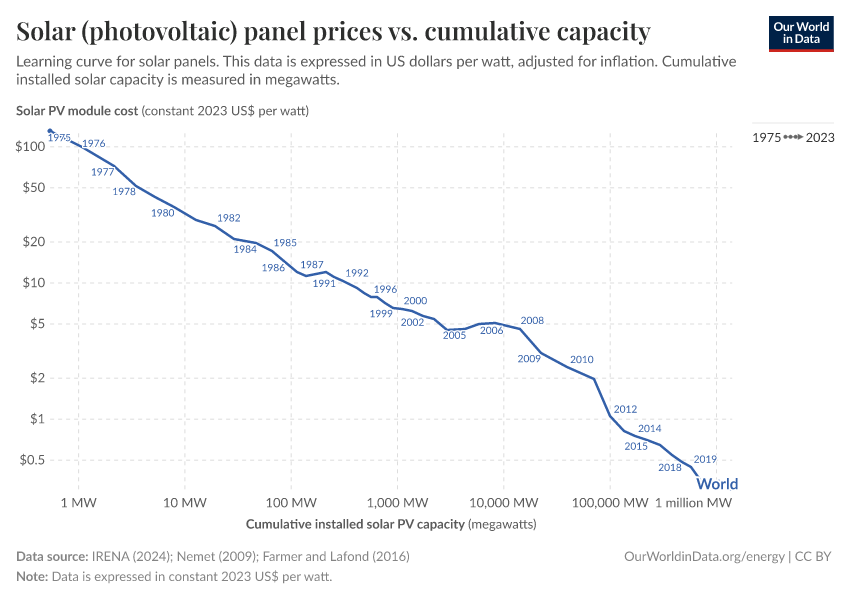
The price of batteries has declined by 97% in the last three decades
Artificial Intelligence (AI) and Communication Technologies
February 07, 2023
AI timelines: What do experts in artificial intelligence expect for the future?
March 29, 2023
Artificial intelligence has advanced despite having few resources dedicated to its development — now investments have increased substantially
November 07, 2019
The importance of social networks for innovation and productivity

September 18, 2019
The rise of social media
Energy and Agricultural Technologies
December 01, 2020
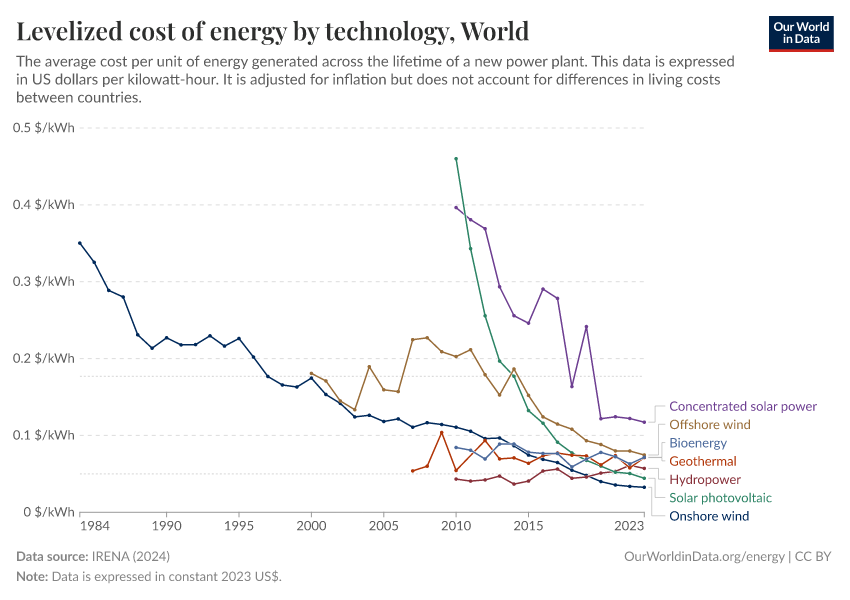
Why did renewables become so cheap so fast?
November 07, 2017
How many people does synthetic fertilizer feed?
August 22, 2017
Yields vs. land use: how the Green Revolution enabled us to feed a growing population
September 13, 2019
The world now produces more seafood from fish farms than wild catch
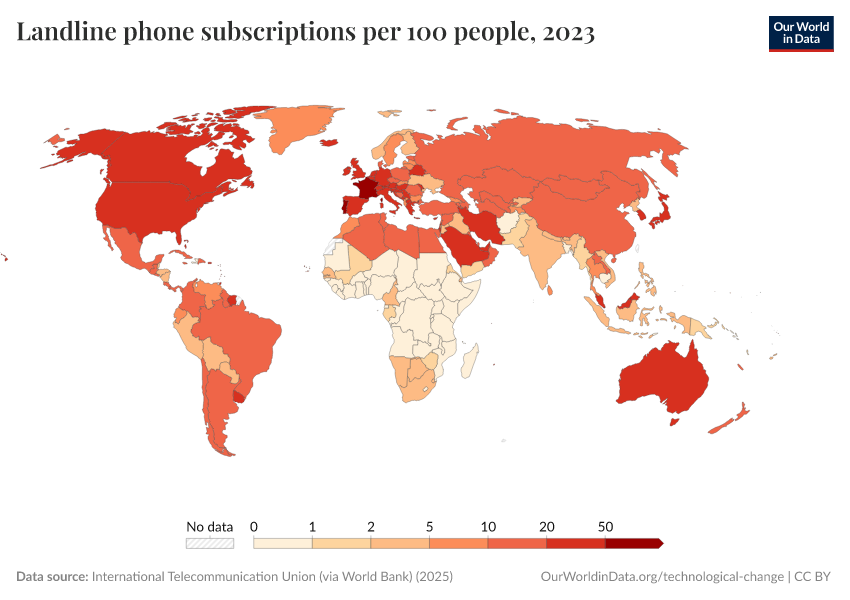
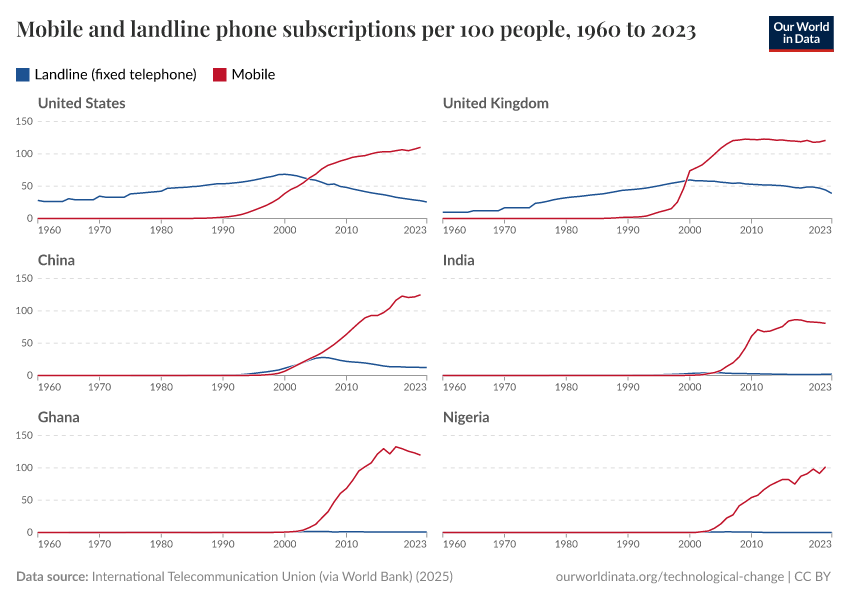
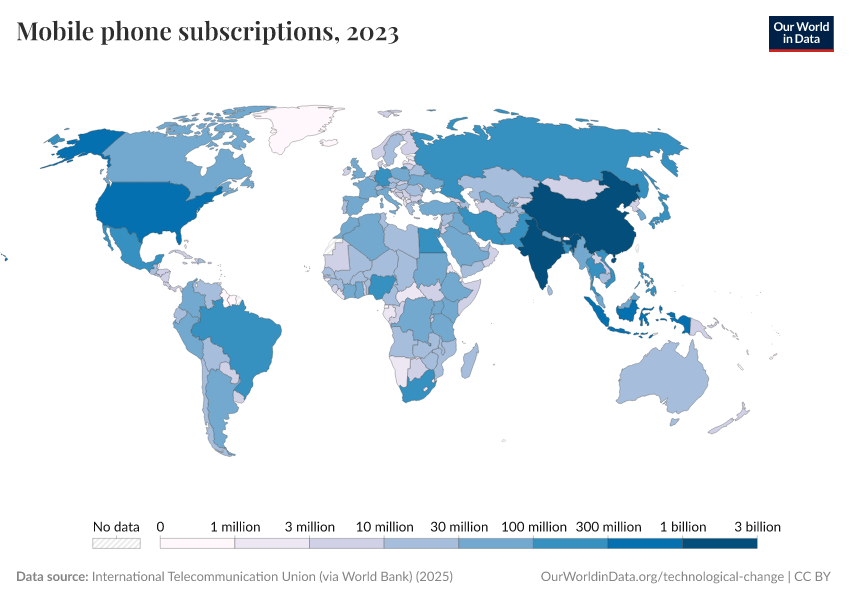
Key Charts on Technological Change
See all charts on this topicCite this work
Our articles and data visualizations rely on work from many different people and organizations. When citing this topic page, please also cite the underlying data sources. This topic page can be cited as:
Max Roser, Hannah Ritchie, and Edouard Mathieu (2023) - “Technological Change” Published online at OurWorldinData.org. Retrieved from: 'https://ourworldindata.org/technological-change' [Online Resource]BibTeX citation
@article{owid-technological-change,
author = {Max Roser and Hannah Ritchie and Edouard Mathieu},
title = {Technological Change},
journal = {Our World in Data},
year = {2023},
note = {https://ourworldindata.org/technological-change}
}Reuse this work freely
All visualizations, data, and code produced by Our World in Data are completely open access under the Creative Commons BY license. You have the permission to use, distribute, and reproduce these in any medium, provided the source and authors are credited.
The data produced by third parties and made available by Our World in Data is subject to the license terms from the original third-party authors. We will always indicate the original source of the data in our documentation, so you should always check the license of any such third-party data before use and redistribution.
All of our charts can be embedded in any site.