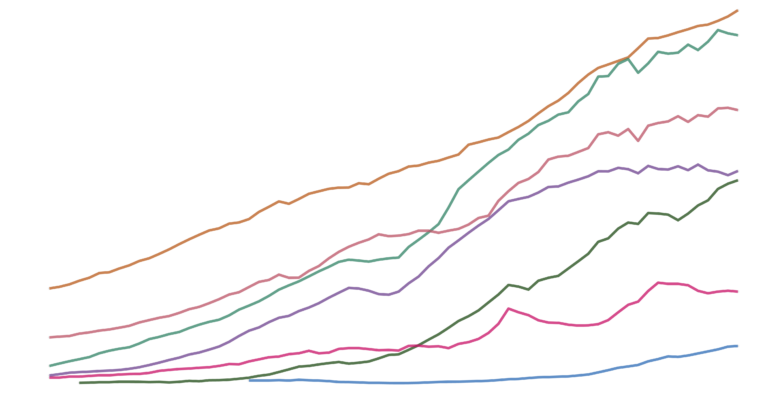
Almost every development that we cover on Our World in Data is underpinned by some form of technological change.
Medical innovations contributed to the decline of child mortality and the improvements in life expectancy. Improved crop yields and reductions in hunger were made possible thanks to the advances in agricultural technologies. The long-term decline of global poverty was primarily driven by increased productivity from technological change. Access to energy, electricity, sanitation, and clean water have transformed the lives of billions. Transport, telephones, and the internet have allowed us to collaborate on problems at a global level.
Emerging technologies are often expensive and therefore initially limited to the richest in society. A key part of technological progress is making these life-changing, and often life-saving, innovations affordable for everyone.
In many ways, technology has transformed our lives for the better. But these developments are not always positive: many of humanity’s largest threats – such as nuclear weapons and potentially also artificial intelligence – are the result of technological advances. To mitigate these risks, good governance can be as important as the technology itself.
On this page, you can find our data, visualizations, and writing on many of the most fundamental technological changes that have shaped our world.