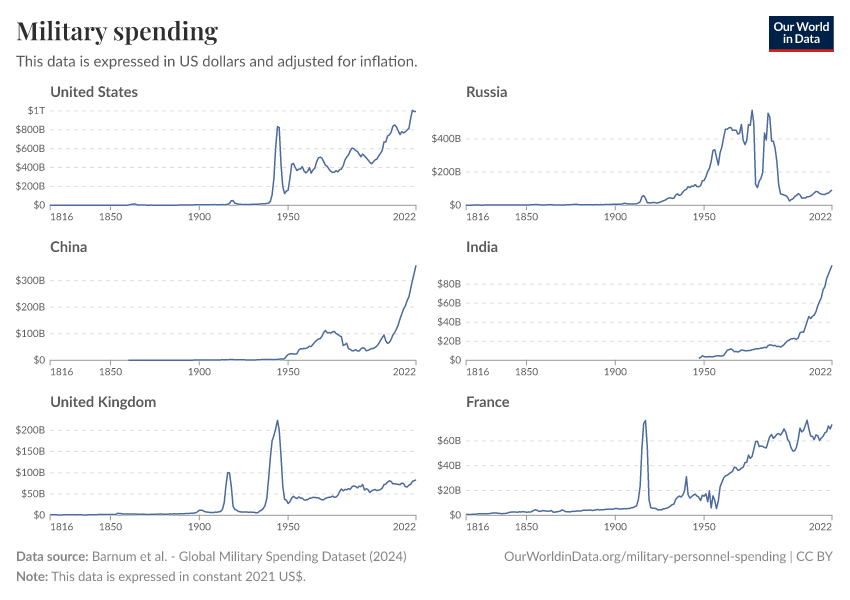
Military spending
What you should know about this indicator
This data is calculated by using nine different military expenditure data sources and combining them using a model. The model links the country-year data together and estimates a mean with a prediction interval for each observation. For more information about the methodology, see the original article.
What you should know about this indicator
This data is calculated by using nine different military expenditure data sources and combining them using a model. The model links the country-year data together and estimates a mean with a prediction interval for each observation. For more information about the methodology, see the original article.
Sources and processing
This data is based on the following sources
How we process data at Our World in Data
All data and visualizations on Our World in Data rely on data sourced from one or several original data providers. Preparing this original data involves several processing steps. Depending on the data, this can include standardizing country names and world region definitions, converting units, calculating derived indicators such as per capita measures, as well as adding or adapting metadata such as the name or the description given to an indicator.
At the link below you can find a detailed description of the structure of our data pipeline, including links to all the code used to prepare data across Our World in Data.
Reuse this work
- All data produced by third-party providers and made available by Our World in Data are subject to the license terms from the original providers. Our work would not be possible without the data providers we rely on, so we ask you to always cite them appropriately (see below). This is crucial to allow data providers to continue doing their work, enhancing, maintaining and updating valuable data.
- All data, visualizations, and code produced by Our World in Data are completely open access under the Creative Commons BY license. You have the permission to use, distribute, and reproduce these in any medium, provided the source and authors are credited.
Citations
How to cite this page
To cite this page overall, including any descriptions, FAQs or explanations of the data authored by Our World in Data, please use the following citation:
“Data Page: Military spending”, part of the following publication: Bastian Herre and Pablo Arriagada (2013) - “Military Personnel and Spending”. Data adapted from Barnum et al.. Retrieved from https://archive.ourworldindata.org/20251209-133038/grapher/military-spending-gmsd.html [online resource] (archived on December 9, 2025).How to cite this data
In-line citationIf you have limited space (e.g. in data visualizations), you can use this abbreviated in-line citation:
Barnum et al. - Global Military Spending Dataset (2025) – with minor processing by Our World in DataFull citation
Barnum et al. - Global Military Spending Dataset (2025) – with minor processing by Our World in Data. “Military spending” [dataset]. Barnum et al., “Global Military Spending Dataset Version 8” [original data]. Retrieved January 20, 2026 from https://archive.ourworldindata.org/20251209-133038/grapher/military-spending-gmsd.html (archived on December 9, 2025).