Our World
in Data
Gdoc/Admin

How epidemiological models of COVID-19 help us estimate the true number of infections

We know that confirmed COVID-19 cases are only a fraction of true infections. How small a fraction though?

By: Charlie Giattino
August 24, 2020
Cite this articleReuse our work freely

A key limitation in our understanding of the COVID-19 pandemic is that we do not know the true number of infections. Instead, we only know of infections that have been confirmed by a test – the confirmed cases. But because many infected people never get tested,1 we know that confirmed cases are only a fraction of true infections. How small a fraction though?

To answer this question, several research groups have developed epidemiological models of COVID-19. These models use the data we have – confirmed cases and deaths, testing rates, and more – plus a range of assumptions and epidemiological knowledge to estimate true infections and other important metrics.

The chart here shows the mean estimates of the true number of daily new infections in the United States from four of the most prominent models.2 For comparison, the number of confirmed cases is also shown.

Click to open interactive version

Two things are clear from this chart: All four models agree that true infections far outnumber confirmed cases. But the models disagree by how much, and how infections have changed over time.

When the number of confirmed cases in the US reached a peak in late July 2020, the IHME and LSHTM models estimated that the true number of infections was about twice as high as confirmed cases, the ICL model estimated it was nearly three times as high, and Youyang Gu's model estimated it was more than six times as high. Back in March the estimated discrepancy between confirmed cases and true infections was even many times higher.

In this post we examine these four models and how they differ by unpacking their essential elements: what they are used for, how they work, the data they are based on, and the assumptions they make.

We also aim to make the model estimates easily accessible in our interactive charts, allowing you to quickly explore different models of the pandemic for most countries in the world. To do this simply click "Change country" on each chart.

Three of the four models we look at are “SEIR”3 models,4 which simulate how individuals in a population move through four states of a COVID-19 infection: being Susceptible, Exposed, Infectious, and Recovered (or deceased). How individuals move through these states is determined by different model “parameters,” of which there are many. Two key ones are the effective reproduction number (Rt)5 – how many other people a person with COVID-19 infects at a given time – and the infection fatality rate (IFR) – the percent of people infected with a disease who die from it.

You can learn more about how SEIR models work by exploring these resources:

Imperial College London (ICL)

Age-structured SEIR model focused on low- and middle-income countries (details as of 23 August 2020)

This chart shows the ICL model’s estimates of the true number of daily new infections in the United States. To see the estimates for other countries click "Change country." The lines labeled “upper” and “lower” show the bounds of a 95% uncertainty interval. For comparison, the number of confirmed cases is also shown.

Click to open interactive version

Website

https://mrc-ide.github.io/global-lmic-reports/

Regions covered

164 countries and territories across the world

Time covered

The first date covered is the estimated start of the pandemic for each country. The model makes projections that extend 90 days past the latest date of update.6

Update frequency

About 2–3 times per week

What is the model?

The model is a stochastic SEIR variant with multiple infectious states to reflect different COVID-19 severities, such as mild or asymptomatic versus severe.

What is the model used for?

ICL describes its model as a tool to help countries understand at what stage the country is in its epidemic (e.g., before or after a peak) and how healthcare demand might change in the future under three policy scenarios. These scenarios are designed to provide a counterfactual of what could happen if current interventions were maintained, increased, or relaxed and are therefore not intended to forecast future mortality.

ICL uses the model estimates to write reports for individual low- and middle-income countries (LMICs) that are relatively early in their epidemics; these reports are focused on the next 28 days. The downloadable model estimates additionally include data for some high-income countries later in their epidemics (e.g., the US and EU countries) and projections 90 days into the future.

Based on the model ICL publishes estimates of the following metrics:

What data is the model based on?

The model is “fit” to data on confirmed deaths7 by using an estimated IFR to “back-calculate” how many infections would have been likely over the previous weeks to produce that number of deaths. It uses mobility data – from Google or, if unavailable, inferred from ACAPS government measures data – to modulate the Rt, the key parameter on how transmission is changing.

Additionally, the model uses age- and country-specific data on demographics, patterns of social contact, hospital availability, and the risk of hospitalization and death, though the availability of this data varies by country.

What are key assumptions and potential limitations?

The model uses an estimated IFR for each country calculated by applying age-specific IFRs observed in China and Europe (of about 0.6–1%) to that country’s age distribution. In countries like many LMICs with younger populations than in China and Europe, this results in IFR estimates of typically 0.2–0.3% because younger populations have lower associated mortality rates. These lower mortality rates, however, assume access to sufficient healthcare, which might not always be the case in LMICs. Differences between the estimated and true IFRs could impact the accuracy of model estimates.

The model assumes that the number of confirmed deaths is equal to the true number of deaths. But research on excess mortality and known limitations to testing and reporting capacity suggest that confirmed deaths are often fewer than true deaths. Where this is the case the model likely underestimates the true health burden.

The model assumes that the change in transmission over time is a function of average mobility trends for places like stores and workplaces but not parks and residential areas.8 If these assumptions about mobility and transmission do not hold, the model might not accurately track the pandemic.

Like all models, this one makes many assumptions, and we cover only a few key ones here. For a full list see the model methods description.

Institute for Health Metrics and Evaluation (IHME)

Hybrid statistical/SEIR model (details as of 23 August 2020)

Update: IHME announced that "after December 16, 2022, IHME will pause its COVID-19 modeling for the foreseeable future."

This chart shows the IHME model’s estimates of the true number of daily new infections in the United States. To see the estimates for other countries click "Change country." The lines labeled “upper” and “lower” show the bounds of a 95% uncertainty interval. For comparison, the number of confirmed cases is also shown.

Click to open interactive version

Website

https://covid19.healthdata.org/

Regions covered

159 countries and territories across the world including subnational data for the US and several other countries

Time covered

The first date covered varies by country. The model makes projections that extend approximately 90–120 days past the latest date of update.

Update frequency

About once a week (though not all countries are updated each time)

What is the model?

The model is a hybrid with two main components: a statistical “death model” component produces death estimates that are used to fit an SEIR model component.

Note that the model has had two significant updates since its initial publication:

What is the model used for?

IHME describes its model as a tool to help government officials understand how different policy decisions could impact the course of the pandemic and to plan for changing healthcare demand.

The model makes deaths projections that have been highly publicized and sometimes criticized.9 Though much of the criticism was leveled at a previous version of the model, known as “CurveFit,” that was used before the SEIR component was added on 4 May. The projections are made under currently three scenarios.10

Based on the model IHME publishes estimates of the following metrics:

What data is the model based on?

The death model uses data on confirmed cases, confirmed deaths,11 and testing.12

The SEIR model is fit to the output of the death model by using an estimated IFR to back-calculate the true number of infections.

The model uses several other types of data to simulate transmission and disease progression: mobility, social distancing policies, population density, pneumonia seasonality and death rate, air pollution, altitude, smoking rates, and self-reported contacts and mask use. Details on the sources of these data can be found on the model FAQs and estimation updates pages.

What are key assumptions and potential limitations?

The model uses an estimated IFR based on data from the Diamond Princess cruise ship and New Zealand. Though IHME does not give numbers for these, the Diamond Princess IFR has been estimated at 0.6% (95% uncertainty interval of 0.2–1.3%).13 Differences between the estimated and true IFRs could impact the accuracy of model estimates.

The death model makes several assumptions about the relationship between confirmed deaths, confirmed cases, and testing levels. For example, that a decreasing case fatality rate (CFR) – the ratio of confirmed deaths to confirmed cases14 – is reflective of increasing testing and a shift toward testing mild or asymptomatic cases. But the CFR could also decrease for other reasons, such as improved treatment or a decline in the average age of infected people.

The model assumes that the change in transmission over time is a function of several data inputs (listed above), like mobility and population density. If these assumptions do not hold – for example, because the data is less relevant or its relationship with transmission is misspecified – the model might not accurately track the pandemic.

More details are discussed in the model FAQs and in different estimation update reports.

Youyang Gu (YYG)

SEIR model with machine learning layer (details as of 23 August 2020)

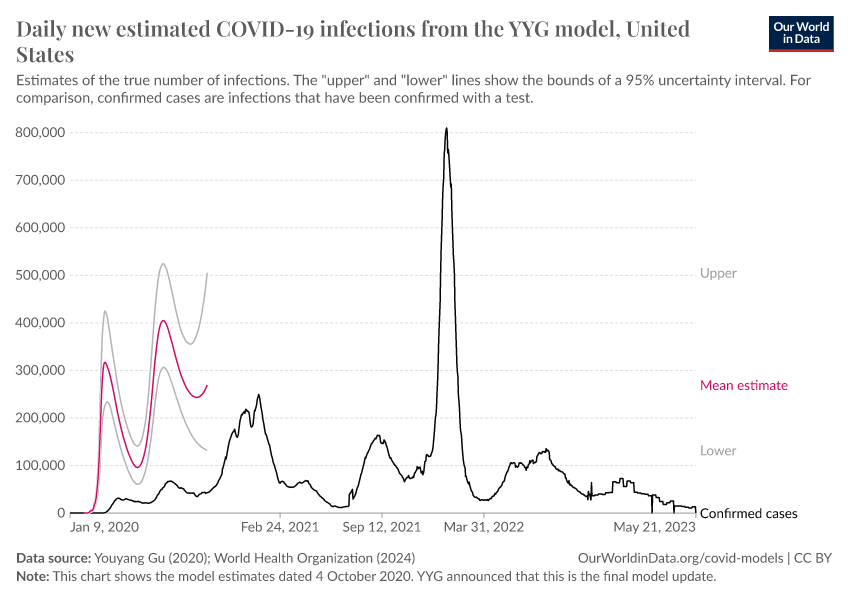
Update: Youyang Gu announced that 5 October 2020 is the final model update

This chart shows the YYG model’s estimates of the true number of daily new infections in the United States. To see the estimates for other countries click "Change country." The lines labeled “upper” and “lower” show the bounds of a 95% uncertainty interval. For comparison, the number of confirmed cases is also shown.

Click to open interactive version

Website

https://covid19-projections.com/

Regions covered

71 countries across the world including subnational data for the US and Canada

Time covered

The first date covered varies by country. The model makes projections that extend approximately 90 days past the latest date of update.

Update frequency

Daily

What is the model?

The model consists of an SEIR base with a machine learning layer on top to search for the parameters that minimize the error between the model estimates and the observed data.

What is the model used for?

Youyang describes his model as making projections of true infections and deaths that optimize for forecast accuracy. Though he also stresses that his projections cover a range of possible outcomes, and that projections are not “wrong” if they help shape a different outcome in the future.

Based on the model Youyang publishes estimates of the following metrics:

The model does not focus on projections under different scenarios, but has explored what would have happened if the US had mandated social distancing one week earlier or one week later, or if 20% of infected people immediately self-quarantined.

What data is the model based on?

The model is fit to data on confirmed deaths15 by using an estimated IFR to back-calculate the true number of infections. Confirmed cases and hospitalization data are sometimes used to help set bounds for the machine learning parameter search.

What are key assumptions and potential limitations?

The model uses an estimated IFR for each region based initially on that region’s observed CFR. The IFR is then decreased16 linearly over the span of three months until it is 30% of its initial value to reflect the lower average age of infections and improving treatments. Currently, the IFR is estimated to be 0.2–0.4% in most of the US and Europe. Differences between the estimated and true IFRs could impact the accuracy of model estimates.

The model assumes there will be unreported deaths for the "first few weeks” of a region’s pandemic, and that this underreporting will decrease until the number of confirmed deaths equals true deaths. As noted before, this is often not the case, and thus the model might underestimate the true health burden.

The model makes assumptions about how reopening will affect social distancing and ultimately transmission. For example, if reopening causes a resurgence of infections, the model assumes regions will take action to reduce transmission, which is modeled by limiting the Rt. It also assumes a reopening date for regions (especially outside the US and Europe) where the true date is unknown.

The model was created and optimized for the US. Thus for other countries the model estimates might be less accurate.

For a full list of assumptions and limitations see the model "About" page.

London School of Hygiene & Tropical Medicine (LSHTM)

Statistical model estimating underreporting of infections (details as of 23 August 2020)

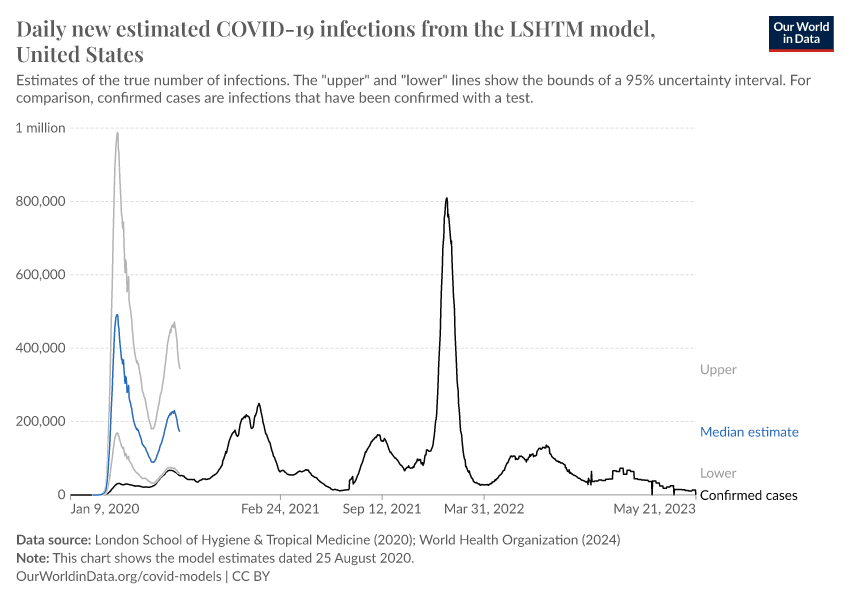
This chart shows the LSHTM model’s estimates of the true number of daily new infections in the United States. To see the estimates for other countries click "Change country." The lines labeled “upper” and “lower” show the bounds of a 95% uncertainty interval. For comparison, the number of confirmed cases is also shown.

Click to open interactive version

Website

https://cmmid.github.io/topics/covid19/global_cfr_estimates.html

Regions covered

159 countries and territories across the world (those with at least 10 confirmed deaths out of a total of 210)

Time covered

The first date covered varies by country. The model does not make projections.

Update frequency

About once a week

What is the model?

The model starts with a country’s CFR and adjusts it for the fact that there is a delay of roughly 2–3 weeks between case confirmation and death (or recovery).17 This delay-adjusted CFR is then compared to a baseline, delay-adjusted CFR to estimate the "ascertainment rate" – the proportion of all symptomatic infections that have actually been confirmed.18

This estimated ascertainment rate is then used to adjust the number of confirmed cases19 to estimate the true number of symptomatic infections. To finally estimate total infections, the symptomatic infections estimate is adjusted to include asymptomatic infections, which are estimated to compose between 10–70% (median 50%) of total infections.20

What is the model used for?

LSHTM describes its model as a tool to help understand the level of undetected epidemic progression and to aid response planning, such as when to introduce and relax control measures.

Based on the model LSHTM publishes estimates of the ascertainment rate.

What data is the model based on?

The model is based on data on confirmed deaths and confirmed cases.21

What are key assumptions and potential limitations?

The model assumes a baseline, delay-adjusted CFR of 1.4% and that any difference between that and a country’s delay-adjusted CFR is entirely due to under-ascertainment. But many other factors likely play a role, such as the burden on the healthcare system, COVID-19 risk factors in the population, the ages of those infected, and more.

The assumed baseline CFR is based on data from China and does not account for different age distributions outside China. This causes the ascertainment rate to be overestimated in countries with younger populations and underestimated in countries with older populations.22

The model assumes that the number of confirmed deaths is equal to the true number of deaths. As noted before, this is often not the case, and thus the model might underestimate the true health burden.

Reported deaths data is sometimes changed retroactively, which can be challenging for the model and might affect its estimates.

More assumptions and limitations are discussed in the full report.

How should we think about these models and their estimates?

All four models we looked at agree that true infections far outnumber confirmed cases, but they disagree by how much. We now have some insight into these differences: The models all differ to some degree in what they are used for, how they work, the data they are based on, and the assumptions they make.

Making these differences transparent helps us understand how we should think about these models and their estimates. For example, understanding that some models are used for scenario planning and not forecasting (like ICL’s) while others are optimized for forecast accuracy (like Youyang’s) puts their estimates in context. And the models all make different assumptions that each have limitations; we can decide if those limitations are relevant to a given situation.

In the end, though, we still want to have confidence that models can track the pandemic accurately. We can calibrate our confidence in different models by giving their estimates a reality check.

One way to do this is to compare model estimates against some observed “ground truth” data. For example, if a model is forecasting the number of deaths four weeks from now, we can wait four weeks and compare the forecast to the deaths that actually occur.23

But sometimes the ground truth is not easily observed, as is the case with the true number of infections. Here we have to look for converging evidence from other research, such as from seroprevalence studies that test for COVID-19 antibodies in the blood serum to estimate how many people have ever been infected.24

By gaining a deeper, more nuanced understanding of these models and their strengths and weaknesses, we can use them as valuable tools to help make progress against the pandemic.

Acknowledgments

We are grateful to the researchers whose work we cover in this article for giving helpful feedback and suggestions. Thank you.

Endnotes

  1. Infected people might not get tested for several reasons, such as not having easy access to testing or not even knowing they are infected because they have no symptoms (though they are still able to transmit the virus). Such asymptomatic infections are estimated to be 10–70% of total infections. Source: CDC COVID-19 Pandemic Planning Scenarios.

  2. There are many models in use besides these four, including other ones by the research groups we cover here. We chose these four models because they are prominent, have been used by policymakers, and have been updated regularly. We use them more for illustration than completeness.

  3. Pronounced by saying each letter, “S-E-I-R.”

  4. The London School model is not an SEIR model.

  5. Also called "time-varying" reproduction number.

  6. While projections are an important aspect of what this and some other models are used for, we do not cover them in this article.

  7. As reported by the European Centre for Disease Prevention and Control (ECDC).

  8. The model assumes that in parks “significant contact events are negligible” and that an “increase in residential movement will not change household contacts.”

  9. For example: Sharon Begley (2020, 17 Apr.) “Influential Covid-19 model uses flawed methods and shouldn’t guide U.S. policies, critics say.” STAT News.

  10. For more details about the scenarios see the model FAQs.

  11. Confirmed cases and deaths data as reported by Johns Hopkins University and several official sources.

  12. As reported by the COVID Tracking Project (for US), official sources (Brazil and Dominican Republic), and Our World in Data (all other countries).

  13. Russell et al (2020). Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship. Eurosurveillance, 25(12). https://doi.org/10.2807/1560-7917.ES.2020.25.12.2000256

  14. The CFR is similar to the IFR but uses the confirmed deaths and cases reported by countries. In contrast, the IFR uses true deaths and infections, which are generally not known and have to be estimated.

  15. As reported by Johns Hopkins University. The data is smoothed before fitting.

  16. Except in “later-impacted regions like Latin America, we wait an additional 3 months before beginning to decrease the IFR.”

  17. The typical CFR calculation divides confirmed deaths by confirmed cases reported on the same day, but those deaths were actually caused by cases confirmed roughly 2–3 weeks before.

  18. All but a trivial number of confirmed cases are assumed to be symptomatic.

  19. This data is first smoothed.

  20. In accordance with this methodology and in consultation with the LSHTM researchers, we perform these calculations to produce the estimates of total infections presented here.

  21. Both as reported by the ECDC.

  22. In a secondary analysis the LSHTM researchers do adjust the baseline CFR for different age distributions. But this has its own assumptions and limitations and is thus not clearly a better approach. More details can be found in the full report.

  23. Though we still need to consider that such forecasts might not track what actually occurs if they help shape a different outcome in the future.

    Some current efforts to score forecasts for accuracy are by Youyang Gu, IHME, The Zoltar Project, and Covid Compare.

  24. The LSHTM researchers, for example, compared their model estimates to seroprevalence estimates and found good agreement. You can read more about this in their full report.

Cite this work

Our articles and data visualizations rely on work from many different people and organizations. When citing this article, please also cite the underlying data sources. This article can be cited as:

Charlie Giattino (2020) - “How epidemiological models of COVID-19 help us estimate the true number of infections” Published online at OurWorldinData.org. Retrieved from: 'https://ourworldindata.org/covid-models' [Online Resource]

BibTeX citation

@article{owid-covid-models,
    author = {Charlie Giattino},
    title = {How epidemiological models of COVID-19 help us estimate the true number of infections},
    journal = {Our World in Data},
    year = {2020},
    note = {https://ourworldindata.org/covid-models}
}
Our World in Data logo

Reuse this work freely

All visualizations, data, and code produced by Our World in Data are completely open access under the Creative Commons BY license. You have the permission to use, distribute, and reproduce these in any medium, provided the source and authors are credited.

The data produced by third parties and made available by Our World in Data is subject to the license terms from the original third-party authors. We will always indicate the original source of the data in our documentation, so you should always check the license of any such third-party data before use and redistribution.

All of our charts can be embedded in any site.