How does age standardization make health metrics comparable?
Age standardization is a statistical method used to compare disease rates, or other health indicators, between populations while accounting for differences in their age structure.
Age standardization can be helpful when comparing rates of health outcomes (for example, deaths from cancer) between populations, because age can be a significant risk factor for many diseases.
Since age structure varies between countries and in the same country over time, this adjustment allows us to see how mortality and morbidity vary without age differences.
Age standardization involves adjusting the observed rates of a particular outcome to a “standard population” with a specific age structure.
Why is it helpful to standardize health metrics for age?
The proportion of people in different age groups in a country is called its "age structure." Countries across the world have significant differences in age structure. For example, only 2% of the population of Uganda is older than 65, against 30% in Japan.
But many diseases or health outcomes occur more frequently as people get older: for example, cancers, heart disease, or dementia.
This difference in age structure means that a condition that affects older people will tend to occur more frequently in the Japanese population than in the Ugandan population, simply because of the higher proportion of older people in the country.
Standardizing the data for age can tell us how a health condition compares between Japan and Uganda if there were no differences in the age structure of the two countries.
What is a crude rate?
A crude rate is the unadjusted rate of a health outcome before any age standardization is applied.
Suppose a researcher wants to compare the death rate from cancer between Japan and Uganda. They would first calculate the death rate of people from cancer in each country.
To calculate this, for each year, the researcher would take the number of people who died of cancer and divide it by the country's population. This is called the crude rate.
This chart shows the crude death rate from cancer in Uganda and Japan, based on Institute for Health Metrics and Evaluation (IHME) data. It is expressed per 100,000 people in the population.
A crude rate is not inaccurate but can give us a biased view of the situation. By comparing the rates of cancer deaths between Uganda and Japan, we may conclude that something in Japan (such as nutrition, lifestyle, or healthcare) is causing many more people to die from cancer than in Uganda.
But we cannot make such a statement based on the crude rate, because the difference in the death rates may be due to Japan’s higher proportion of older people compared to Uganda.
If we want to accurately compare the rates of a health outcome that becomes more frequent with age, we need to apply age standardization by adjusting these rates to a standard population.
What is a standard population?
We need a “standard population” to apply age standardization. A standard population is a specific age structure used as a reference for these adjustments.
Many different standard populations can be used. Some of the most commonly used ones are the World Standard Population (published by the WHO) and the European Standard Population (published by Eurostat).
There are also national standard populations that can be used to compare health outcomes between different locations within a country. For example, the US National Cancer Institute maintains a standard population for the United States.
In a standard population, age groups are often broken down into 5-year intervals. Next to each age group, the proportion that the age group represents in the standard population is given.
For example, in the WHO’s World Standard Population, the under-5 age group represents 8.86% of the standard population, the 5 to 9 years age group represents 8.69% of the standard population, etc.
How does age standardization work?
Age standardization is applied in three steps.
(1) Researchers start with the observed rates of the relevant health outcome for each age group. In our example, these would be the cancer death rates for each age group in Japan and Uganda.
For example, if we have 5-year intervals in our standard population, we would start from the cancer death rates of people in Japan aged 0–4, 5–9, 10–14, etc. These rates are called age-specific rates.
(2) These rates are then multiplied by the proportion of the corresponding age group in the standard population. For example, as the group aged 60–64 represents 3.72% of the World Standard Population, we would multiply the age-specific rate for this group by 3.72%.
(3) After multiplying all age-specific rates by the corresponding proportion of each age group in the standard population, we sum the rates to obtain one number. This number is the age-standardized rate.1
These age-standardized rates allow us to compare cancer death rates in Uganda and Japan as if they applied to two countries with identical age structures.
In this example, we see that Uganda's age-standardized cancer death rate has surpassed Japan's since 2000.
Age-standardized rates provide a better comparison between populations with different age structures but do not represent the actual rate in each population. Using the age-standardized rate to say that 114 per 100,000 people in the Japanese population die from cancer each year would be inaccurate. We should refer back to the crude rate (346 per 100,000) for this.
Age standardization can also be used across time or within a country
Age standardization is often used to compare health metrics between countries.
But we can also use it to measure health outcomes in the same location over time. Again, if we have a disease that primarily affects older people, we expect rates of that disease to rise over time as populations age.
Age standardization then allows us to see how the rate would have changed if the population's age structure hadn’t changed.
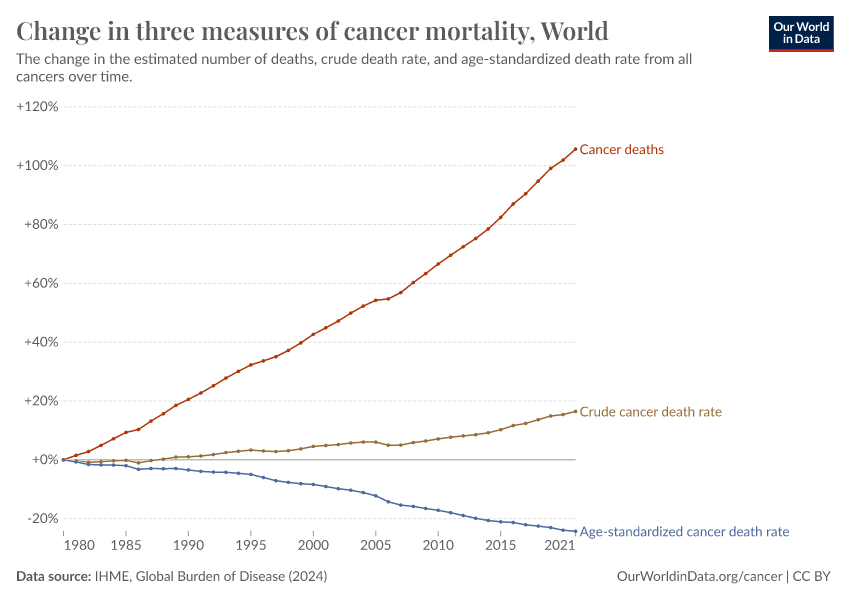
This can have a significant impact on our interpretation of health outcomes. One example of this comes from global death rates from cancer. On this chart, you can see that if we look at crude death rates (without age standardization), it looks like they have increased a lot in recent decades.
But a big part of this effect is explained by the fact that the world is getting older. When we adjust for age, we see that death rates have fallen.
In this related post, we discuss this chart – and the question of whether or not the world is making progress against cancer – in more detail.
Endnotes
The national statistical office of Canada provides more details and a full example of how to calculate age-standardized rates.
Cite this work
Our articles and data visualizations rely on work from many different people and organizations. When citing this article, please also cite the underlying data sources. This article can be cited as:
Edouard Mathieu (2023) - “How does age standardization make health metrics comparable?” Published online at OurWorldinData.org. Retrieved from: 'https://ourworldindata.org/age-standardization' [Online Resource]BibTeX citation
@article{owid-age-standardization,
author = {Edouard Mathieu},
title = {How does age standardization make health metrics comparable?},
journal = {Our World in Data},
year = {2023},
note = {https://ourworldindata.org/age-standardization}
}
Reuse this work freely
All visualizations, data, and code produced by Our World in Data are completely open access under the Creative Commons BY license. You have the permission to use, distribute, and reproduce these in any medium, provided the source and authors are credited.
The data produced by third parties and made available by Our World in Data is subject to the license terms from the original third-party authors. We will always indicate the original source of the data in our documentation, so you should always check the license of any such third-party data before use and redistribution.
All of our charts can be embedded in any site.